役に立たない情報

_ [R基礎] なんでRを使うのか？

Rってあんじゃん？卒論とかのデータをまとめるのにすげー便利なんだけど，みんなあんまり使わないんだよね．みんなxlsとかのファイルとか使う．

もうね正直やめてほしい．

スクリプトベースでデータ加工方法を残せるからRの方がいいんだよ．再現性も担保できるし，生データをcsv形式でもテキストベースでも残せちゃう．まあxlsでも残せるっちゃ残せるんだけど他のファイルへのリンクってディレクトリ管理が面倒になるので，なるべくポータビリティを考えてほしい．君ら学生ってすぐ卒業しちゃうし．

んでね，このblogでもRの使い方，Tipsみたいなものをちょこちょこ書いていくから覚悟しろこのやろ．

_ [R基礎] Rをスクリプトで実行する方法

普通さRってコマンドを実行するかR Studioを使うか，まあいずれにしてもRアプリケーション関連のアプリでしか実行できないよねって思っている初学者が多い．まあそうだよね．インタラクティブに使うならいいんだけど，ちょっとなれてきたり，大きな行列とか扱いだすと面倒なんだよね正直．

で，Rってスクリプト言語だって言ってるからスクリプトとして書いて動かしたいじゃん？

[kido@localhost ~]$ Rscript hoge.R

とかするとhoge.Rに書かれたスクリプトが実行されちゃう．Rscriptってコマンドの存在を知れば，まあこれはわかる． で，他にもこんな書き方もできる．

hoge.Rを以下のように書く

#!/usr/bin/Rscript
a <- c("hoge", "hoge", "hoge")

んでhoge.Rに実行権限あたえてちゃうと，

[kido@localhost ~]$ ./hoge.R

で実行できちゃう．

_ [R基礎] Rscriptで実行したスクリプトの中で実行引数を取得する

せっかくスクリプトにしたんだから入力ファイル名とか引数で渡したいじゃん？スクリプトの中にハードコードしちゃうと汎用性下がるし． そんな時はcommandArgs()って関数を呼ぶといいよ．以下のようにhoge.Rを書く．

#! /usr/bin/Rscript

args <- commandArgs()
args

って書いて実行しちゃう．

[kido@localhost ~]$ ./hoge.R p0 p1 p2
[1] "/usr/lib/R/bin/exec/R" "--slave"               "--no-restore"
[4] "--file=./hoge.R"       "--args"                "p0"
[7] "p1"                    "p2"

こんな感じで表示される．つまりRscript実行パラメータの後にからユーザが渡した引数が得られるということがわかる．もちろん

#! /usr/bin/Rscript --vanilla

とかで渡した引数ももちろんこれで取得できるんだけど，できればユーザが渡した引数，p0, p1, p2だけほしいよね？そういう場合は，

#! /usr/bin/Rscript

args <- commandArgs(trailingOnly=TRUE)
args

としてtrailingOnlyをTRUEにしてcommandArgs関数を呼ぶといいよ．そうすると

[kido@localhost ~]$ ./hoge.R p0 p1 p2
[1] "p0" "p1" "p2"

てな感じでユーザ引数だけ取れるよ．便利だね！

参考文献：R documentation, commandArgs

_ [R基礎] データフレームの作り方

とりあえずRで何かデータを扱うとき，データフレームを扱えなければ話にならないのね．CSVからでもデータを読むととりあえずデータフレームに収まっちゃう．で，Rって便利なので２次元マトリクス状のデータフレームは普通に作れちゃうんだけど，それを扱う方法をまず書いておく．

で，行列はc関数でさっくり作れるのね．

> x <- c(160,171,165,150,148,183)
> y <- c(70,68,49,49,50,78)
> z <- c(0,0,1,1,NA,0)

NAってのは欠損値のことで，スパースなデータってのは実験上わりと出てくる．例えばRでCSVからファイルを読み取る場合，欠損値のところはNAになる．んで，この欠損値が入ったまま検索すると期待した結果が得られないのね．NAは欠損値（NULLではない）だから検索結果にNAの行が入ってくる．

とりあえず上のx, y, zをデータフレームにして表にしてみよう

> db <- data.frame("height"=x, "weight"=y, "s"=z)
> db
  height weight  s
1    160     70  0
2    171     68  0
3    165     49  1
4    150     49  1
5    148     50 NA
6    183     78  0
>

_ [R基礎]データフレームでNAがある場合の検索

んで，これをs==1とかで検索するとこうなる

> db[db$s==1,]
   height weight  s
3     165     49  1
4     150     49  1
NA     NA     NA NA
>

これだと検索結果にNAの行が出てくるので，こんなデータは普通いらないよね？で，データフレーム内のNAが含まれている行をすべて削除する場合は

> db <- db[complete.cases(db),]

もしくはdb$sのNAだけを削除したい場合は

> db <- db[!is.na(db$s),]

こうするとNAが含まれる行を削除してくれる．

> db[db$s==1,]
  height weight s
3    165     49 1
4    150     49 1

いいね！

参考文献：R documentation, complete.cases, R documentation, is.na

_ [R基礎] 散布図の作り方

データの分散をただ散布図で出したい！そんな時あるよね．うんうん卒論てカサ増しが大事だしね． でね，適当な実験データの散布図を書こうとするのもRって便利なんだよ．

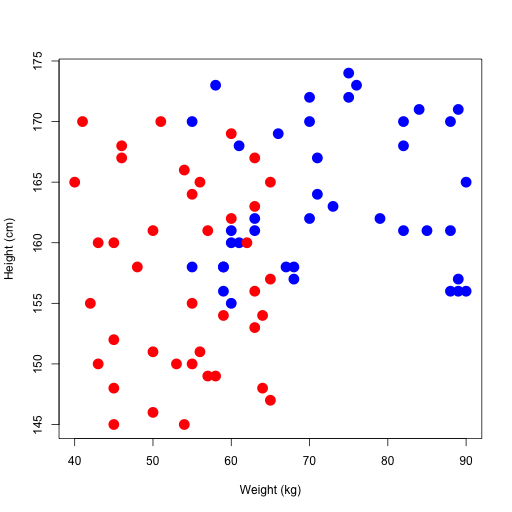
例えば成人男子の体重と身長，成人女子の体重と身長をプロットしたい場合，CSVから読み込みでもいいんだけど，適当にデータフレームに突っ込むじゃん？

m_h: 男子身長, m_w: 男子体重

f_h: 女子身長, f_w: 女子体重

とするじゃん？

plot(0,0,type="n",xlim = c(min(m_w,f_w), max(m_w,f_w)), ylim = c(min(m_h,f_h), max(m_h,f_h)),xlab="Weight (kg)",ylab="Height (cm)")
points(m_w,m_h,pch=16,col="#0000ff",cex=2)
points(f_w,f_h,pch=16,col="#ff0000",cex=2)

とこんな感じで書ける．

_ [R基礎] これだと不親切なのでちょっとランダムにサンプリングを作る方法も書いておく

とりあえず一番簡単な無作為な（無意味な）行列を作るにはsample関数を使うと良い．

m_h <- sample(155:175, 40, replace=TRUE)
m_w <- sample(55:90, 40, replace=TRUE)
f_h <- sample(145:170, 40, replace=TRUE)
f_w <- sample(40:65, 40, replace=TRUE)

という風にm_hだと，155から175の範囲の40の要素を無作為に抽出してデータフレームにしてくれる．これを上のplotと組み合わせて，適当な散布図を書くことができるよ．

あとさらっとpngでファイル出力もしちゃうスクリプトをサンプルで載せておくね！じゃあね！

#!/usr/local/bin/Rscript

m_h <- sample(155:175, 40, replace=TRUE)
m_w <- sample(55:90, 40, replace=TRUE)
f_h <- sample(145:170, 40, replace=TRUE)
f_w <- sample(40:65, 40, replace=TRUE)

png("scatter_plot.png", width=512, height=512)

plot(0,0,type="n",xlim = c(min(m_w,f_w), max(m_w,f_w)), ylim = c(min(m_h,f_h), max(m_h,f_h)),xlab="Weight (kg)",ylab="Height (cm)")
points(m_w,m_h,pch=16,col="#0000ff",cex=2)
points(f_w,f_h,pch=16,col="#ff0000",cex=2)

dev.off()

_ [子供の数学] とある確率の問題

A, B, C, Dの4人が，横1列に並んだ5つの椅子に座るとき，Aのすぐとなりの椅子にBが座る確率を求めなさい．

という問題があった．これね．表記がすごい難しいの．何が難しいってAのすぐとなりの椅子にBが座るってところ．

普通に考えると4人が5つの席に座るパターンの全通りは，

5! = 5 x 4 x 3 x 2 x 1 = 120

で，AとBが間隔開けずに隣りに座るパターン数は，AとBを1人として，4つの椅子に座るパターンの全数である4!を出せばいい．AとB，BとAの２つのパターンがあるから2倍して

4! x 2 = 48

となる．だから確率としては，

48 / 120 = 0.4

が答えになるんだよね．でもこれの答えって実は0.5らしいんだよ．まあそうだよね．これだと5人が5つの椅子に座るときにA,Bが隣り合う確率を出しているだけで，問題をあえて4人にする必要性がない．でもすぐ隣の椅子って書いてあんだよね．こんな明確な表現をしているのに難しい問題にしやがる． 普通，問題を難しくするときってわざと明確に書かないでぼやかすことで，集合を大きくするんだよね．こんな出題表現はあんまり見ないんだけどなぁ．

で，それを踏まえた上で答えを書くと，要するにA,○,Bという，Aの隣が空いているけど，その更に隣の椅子にBが座るパターンもAのすぐとなりの椅子にBが座るに含めると，

3! x 2 = 12

という数が含まれることになる．だから確率は，

(48 + 12) / 120 = 0.5

となる． 最近の問題は難しいなぁ．というか教師の国語力の問題なのかなぁ．